PhD
Statistical Genetics: Understanding Polygenic Disease
During my PhD, I worked in statistical genetics—a field focused on understanding how genetic variation influences complex human traits and diseases. This page explains the background, methods, and applications that formed the core of my doctoral research.
Overview of my thesis work
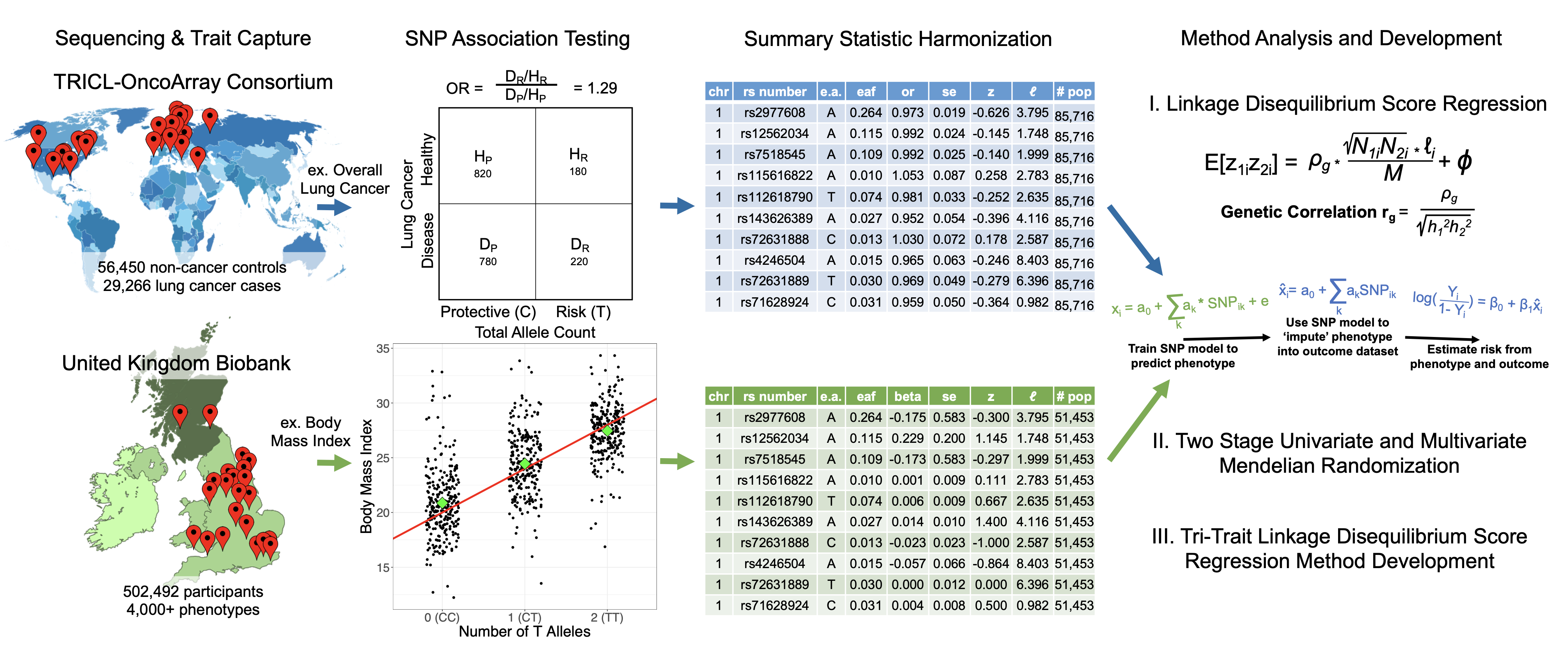
This diagram shows the analytical pipeline I developed, from large-scale genomic datasets (TRICL-OncoArray Consortium and UK Biobank) through statistical harmonization to the application of linkage disequilibrium score regression and Mendelian randomization methods.
The shift from single-gene to polygenic disease
For most of medical genetics’ history, we focused on diseases caused by mutations in single genes—conditions like sickle cell anemia, cystic fibrosis, or Huntington’s disease. These follow clear inheritance patterns and have dramatic effects: if you inherit the wrong version of one gene, you get the disease.
But most common diseases and traits don’t work this way. Height, body mass index, blood pressure, diabetes, heart disease, cancer—these are polygenic. Instead of being caused by one gene with a large effect, they’re influenced by thousands of genetic variants scattered across the genome, each contributing a small effect.
Think of it this way: your height isn’t determined by a single “height gene.” Instead, there are thousands of genetic variants that each nudge your height up or down by tiny amounts—maybe a few millimeters each. Add up all these small effects across the genome, and you get your actual height.
This polygenic architecture is why these traits show continuous variation in the population and why they “run in families” but don’t follow simple inheritance patterns. It’s also why understanding them requires statistical methods that can handle the combined effects of many genetic variants simultaneously.
Genome-wide association studies: Finding the variants that matter
To understand polygenic traits, we need to identify which of the millions of genetic variants in the human genome actually influence the trait we’re studying. This is where genome-wide association studies (GWAS) come in.
A GWAS compares the genetic profiles of people with and without a trait or disease. For each of the millions of genetic positions we can measure, we ask: “Is this variant more common in people with the disease than in people without it?”
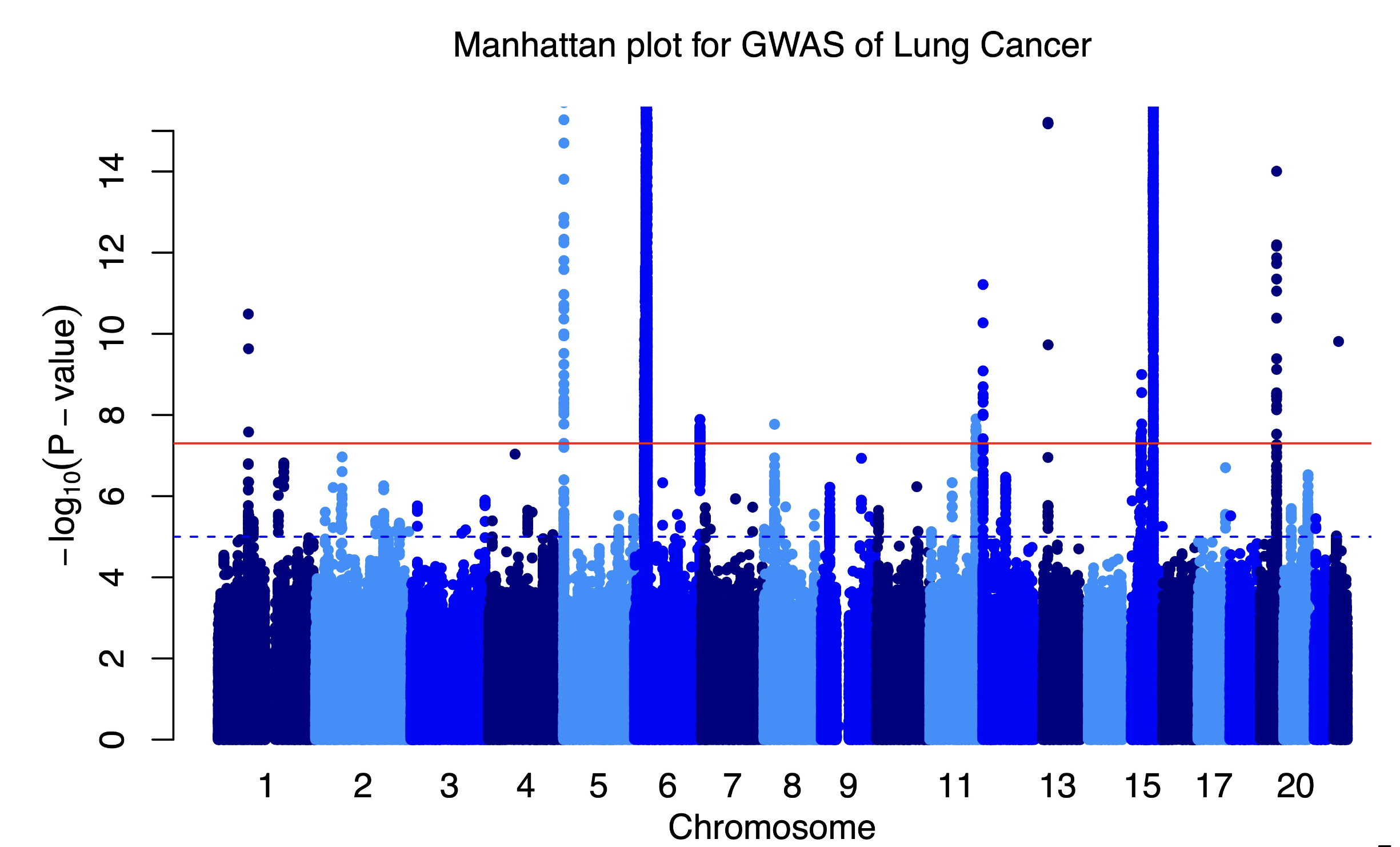
This Manhattan plot shows what GWAS results look like. Each dot represents one genetic variant, plotted by its position in the genome (x-axis) and how strongly it’s associated with the trait (y-axis). The peaks above the red line represent variants that are significantly associated with the trait.
The key insight from GWAS is that for polygenic traits, you see many of these peaks scattered across the genome—not just one or two large effects, but hundreds or thousands of small ones.
The challenge: Linkage disequilibrium and confounding
GWAS results aren’t straightforward to interpret because of linkage disequilibrium (LD)—the fact that nearby genetic variants are correlated with each other. When you inherit a chromosome from your parent, you don’t get a random mix of variants; you inherit them in blocks.
This creates a problem: if a causal variant increases disease risk, all the variants correlated with it will also appear to be associated with the disease, even though most of them aren’t actually doing anything. So a single causal variant can create dozens or hundreds of apparent associations.
Additionally, different human populations have different patterns of genetic variation due to evolutionary history. If your study inadvertently includes more people of one ancestry in the disease group, you can get false associations that reflect population differences rather than biology.
These issues create statistical noise that makes it difficult to separate real biological signals from artifacts.
Linkage disequilibrium score regression: Separating signal from noise
This is where linkage disequilibrium score regression (LDSC) becomes essential. LDSC is a method that can separate true polygenic signal from various forms of confounding by leveraging the structure of linkage disequilibrium.
The key insight is that if a trait is truly polygenic, then genetic variants in high-LD regions should show stronger associations on average, because they “tag” more causal variation. Variants in low-LD regions should show weaker associations. But confounding factors like population stratification affect all variants equally, regardless of their LD.
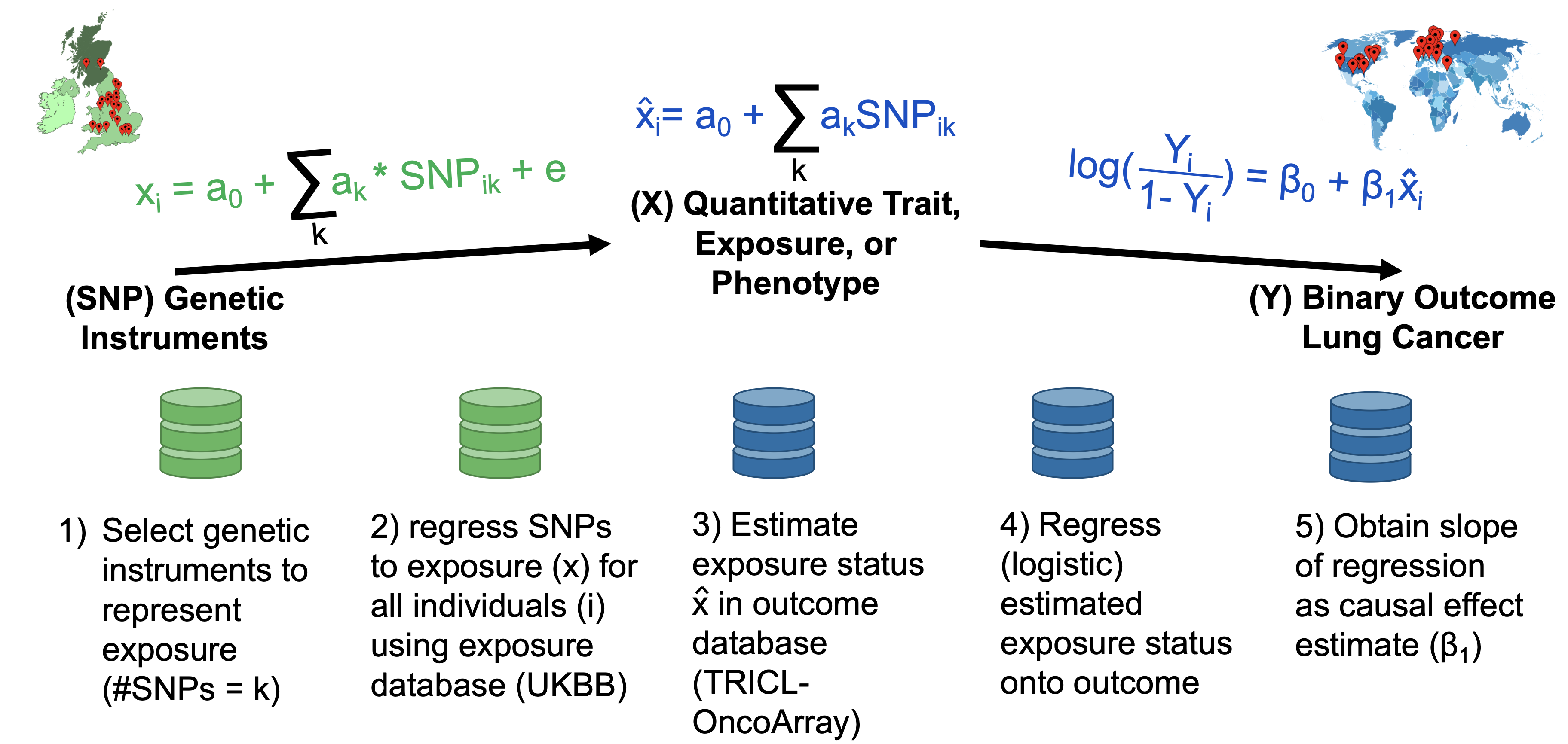
This figure shows how LDSC works and how it can be applied. The method regresses GWAS test statistics on LD scores to estimate heritability and genetic correlations. It can also be used to build polygenic scores in one dataset and apply them to another—essentially creating a genetic predictor of a trait based on the combined effects of many variants.
LDSC tells us several important things: - SNP-heritability: What fraction of trait variation is captured by common genetic variants - Genetic correlation: How much genetic overlap exists between different traits - Partitioned heritability: Which parts of the genome (gene regions, regulatory elements, etc.) contribute most to heritability
Mendelian randomization: Using genetics to infer causation
Understanding genetic architecture is important, but often we want to know about causation. If two traits are genetically correlated, does one cause the other, or do they share common underlying factors?
This is where Mendelian randomization (MR) comes in. MR uses genetic variants as “instrumental variables” to infer causal relationships between traits. The key insight is that genetic variants are randomly assigned at conception, making them largely free from the environmental confounding that plagues observational studies.
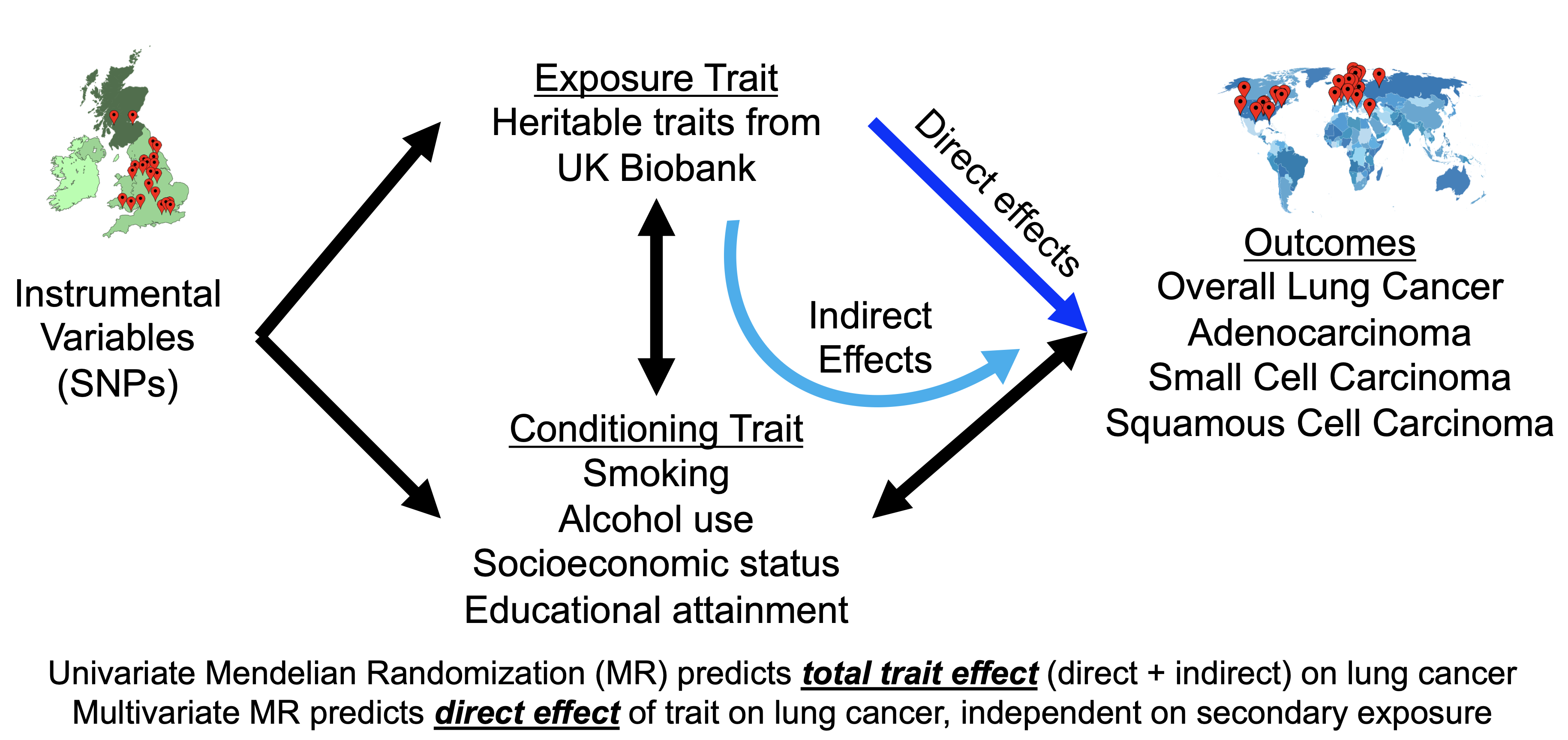
This figure shows a multivariable MR analysis using instrumental variables. In multivariable MR, we can simultaneously estimate the causal effects of multiple related exposures on an outcome, accounting for their correlations. Each point represents a genetic instrument, and the analysis estimates causal effects while controlling for pleiotropy and other violations of MR assumptions.
The logic is straightforward: if a genetic variant increases smoking behavior and also increases lung cancer risk, and the only plausible way it could affect cancer is through smoking, then we have evidence that smoking causes lung cancer.
My research: Applying these methods to lung cancer genetics
My thesis work applied these methods to understand the genetic architecture of lung cancer and its relationship with behavioral and socioeconomic factors. This was particularly challenging because smoking is such a dominant risk factor that it creates confounding throughout the genome.
I used data from major consortia including TRICL (Transdisciplinary Research in Cancer of the Lung), OncoArray, and UK Biobank to investigate several questions:
Genetic architecture characterization: Using LDSC, I estimated the heritability of different lung cancer subtypes and quantified their genetic correlations with other traits. This revealed that lung cancer shares genetic architecture with smoking behavior, educational attainment, and other cancers, but the patterns differ across histological subtypes.
Separating direct from mediated effects: I developed an approach to distinguish genetic effects that operate directly on cancer biology from those that work through smoking behavior. By comparing analyses before and after excluding genomic regions around known smoking-associated variants, I could quantify how much of lung cancer’s genetic signal operates independently of smoking pathways.
Causal inference: I conducted comprehensive MR analyses linking behavioral exposures (smoking intensity, educational attainment, alcohol consumption) to lung cancer outcomes. This involved testing multiple MR methods, extensive sensitivity analyses, and subtype-specific analyses.
Key findings included the characterization and quantification of genetic architecture across lung cancer subtypes, detailed annotation of which genomic regions contribute to heritability, robust quantification of complex trait relationships with lung cancer using UK Biobank data, and evidence that different subtypes have varying degrees of smoking-mediated versus direct genetic effects. The work also involved methodological improvements to existing analytical pipelines.
This work taught me R and Python programming, advanced statistical methods, database management, command-line data wrangling, and machine learning approaches. The interdisciplinary combination of method development, large-scale data analysis, and biological interpretation was exactly the kind of computational problem-solving I found most engaging.
Selected publications
Pettit, R., Byun, J., Han, Y., et al. (2023). “Heritable traits and lung cancer risk: a two-sample mendelian randomization study.” Cancer Epidemiology, Biomarkers & Prevention, 32(10), 1421-1435.
Pettit, R., & Amos, CI. (2022). “Linkage disequilibrium score statistic regression for identifying novel trait associations.” Current Epidemiology Reports, 9(3), 190-199.
Pettit, R., Byun, J., Han, Y., et al. (2021). “The shared genetic architecture between epidemiological and behavioral traits with lung cancer.” Scientific Reports, 11(1), 17559.
Mentorship
I worked with Prof. Chris Amos, who directs quantitative sciences and leads large-scale oncology genetics programs at Baylor College of Medicine (profile). His expertise in large-scale genomic analyses and cancer epidemiology was instrumental in developing robust analytical approaches.
Technical resources
The methods described here build on established software: - LDSC: https://github.com/bulik/ldsc - Python implementation for heritability and genetic correlation - TwoSampleMR: https://github.com/MRCIEU/TwoSampleMR - R package for Mendelian randomization analyses
Key references
Foundational papers: - Bulik-Sullivan, B.K., et al. (2015). “LD Score regression distinguishes confounding from polygenicity in genome-wide association studies.” Nature Genetics, 47(3), 291-295. - Davey Smith, G. & Hemani, G. (2014). “Mendelian randomization: genetic anchors for causal inference in epidemiological studies.” Human Molecular Genetics, 23(R1), R89-R98. - Finucane, H.K., et al. (2015). “Partitioning heritability by functional annotation using genome-wide association summary statistics.” Nature Genetics, 47(11), 1228-1235.